UE simulation
Module n°3 - Model Checking
Hélène Coullon (inspiré du cours de Simon Robillard)
Description du module
Informations générales
- 2 séances de 3h45 avec
- cours
- tutoriel
- mini-projet en séance
- Evaluation par mini-projet en séance
- Contact : helene.coullon@imt-atlantique.fr, bureau B220
Contenu de la séance 1
- Cours Model Checking
- Tutoriels sur Roméo
- construire un réseau de Petri
- simuler un réseau de Petri
- vérifier une propriété
- Mini-projet (par groupes)
- choix de votre système
- spécification en langage naturel
- spécification en réseau de Petri du système
Contenu de la séance 2
- Questions cours
- Mini-projet (par groupes)
- fin spécification en réseau de Petri du système
- propriétés et correction du système
- préparation de l’oral (prévoyez au moins 1h)
- oral (15 minutes par groupe, total 1h30/2h)
Evaluation 1/2
Mini-projet : 6 groupes (un de 4, cinq de 5)
- CG1 Comprendre et analyser, synthétiser un problème et/ou une situation complexe
- CG4 Critiquer et décider
- CG14 S’engager (évaluation dans les séances)
- CG9 Communiquer (oral en séance)
Evaluation 2/2
Attendues pour l’oral
- présenter votre système en langage naturel
- démonstration : modélisation dans Roméo
- présenter vos propriétés
- démonstration : vérification dans Roméo
Introduction
Modélisation
Expliquer le fonctionnement d’un système en langage naturel
- exemple : documentation
- avantages : facile à lire et comprendre par un humain
- désavantages : peu fiable et peut être compris de différentes façons
Modélisation
Modéliser formellement le système
- exemples : réseau de Petri, automates
- avantages : fiable et précis
- désavantages : difficile pour un humain
Test
Approche traditionnelle pour vérifier un système
- facile à mettre en oeuvre
- utile à différentes étapes de la conception
Limitation : Exhaustivité des tests est souvent impossible
“Tester des programmes peut être un moyen très efficace de révéler des bugs, mais est irrémédiablement inadapté pour en démontrer l’absence.” E.W. Dijkstra
Indéterminisme et test
Un système est indéterministe si une exécution depuis un état donné peut mener à plusieurs état différents
Exemples : hasard, éléments externes au système, ordre d’exécution
L’indéterminisme augmente la difficulté des tests
Méthodes formelles
- représentation et modélisation abstraite et formelle du système
- techniques de raisonnement mathématiques sur le modèle pour en vérifier des propriétés
Méthodes formelles
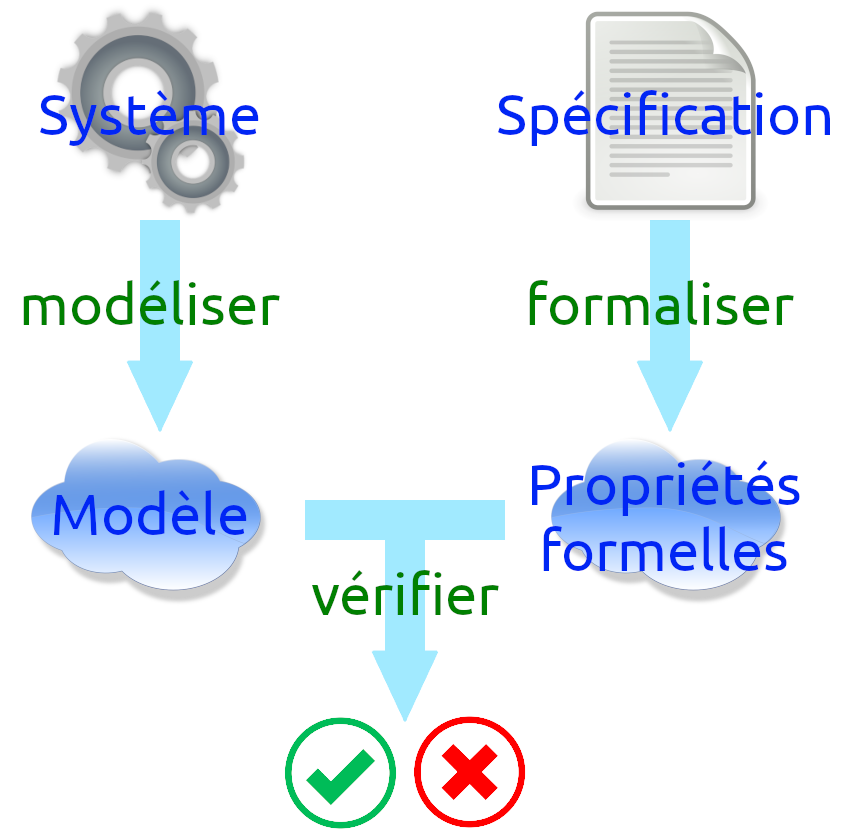
Nous allons utiliser une méthode formelle appelée un Model-Checker
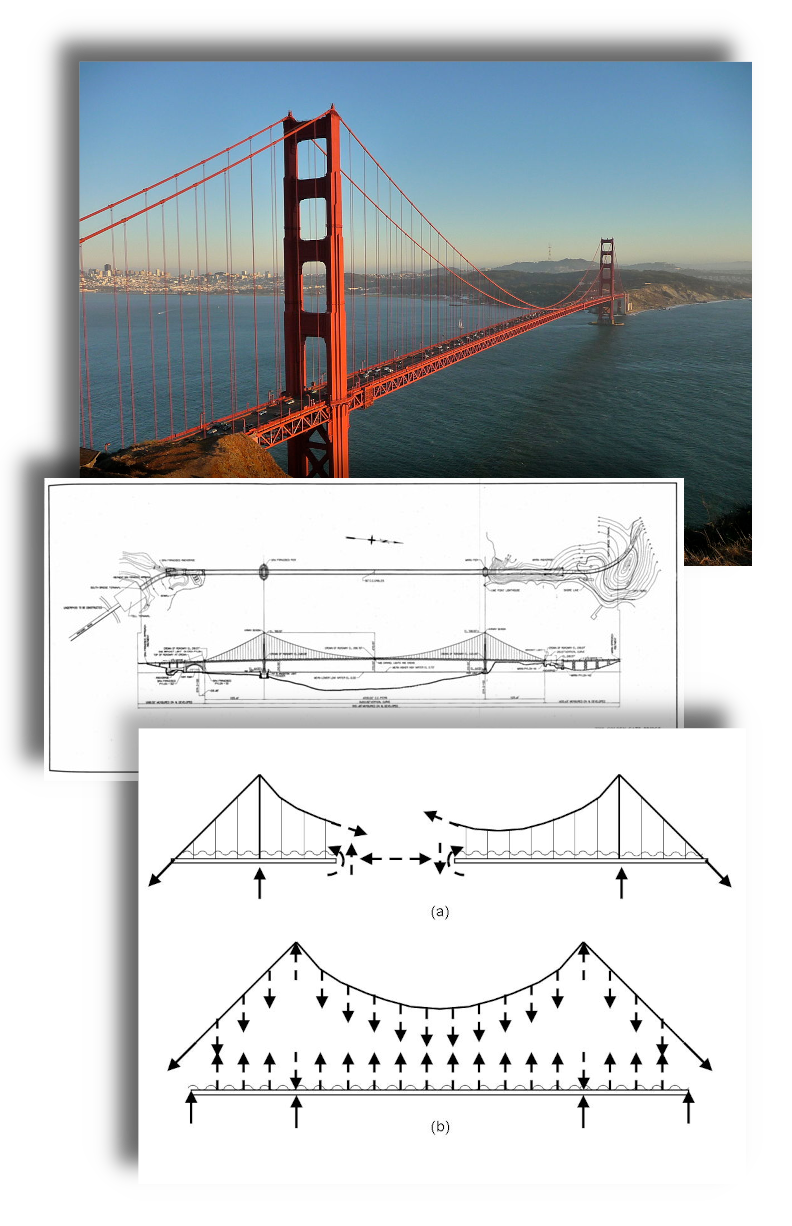
Analogie en physique
- système : un pont
- proriété : resister à des vents violents
- tests : tests en soufflerie sur une maquette
- méthode formelle : modéliser le pont et le vent et étudier mathématiquement la propriété
Outils de modélisation
Vous avez vu dans cette UE par exemple :
- la simulation à événements discrets
- les réseaux de Petri
Vocabulaire propriétés
- safety : proriétés de sûreté
- le système n’entre jamais dans un état non-sûr
- liveness : propriétés de vivacité
- le système finira par atteindre un état désiré
Langages de propriétés
Il existe également différents langages pour exprimer les propriétés formelles
Pour le Model-Checker nous allons utiliser :
Computational Tree Logic (CTL) qui permet d’exprimer des propriétés formelles temporelles sur un réseau de Petri notamment
Partie 1
Logique temporelle
Une logique temporelle décomposée en deux parties :
- langage pour décrire les propriété du système à un instant donné
- “la place P contient n jetons”
- “aucune transition ne peut être franchie”
- ajout de modalités temporelles
- “il est possible que …”
- “il est certain que …”
- “… toujours …”
- “… à un moment …”
Propriétés du système
Cas particulier des réseau de Petri :
Generalized Mutual Exclusion Constraints (GMEC)
- le marquage M (nb jetons)
- identification des places et transitions par un nom
- innégalités (<, <=, >, >=, ==, !=)
- opérateurs Bouléens (and, or, not)
markingBounded(k)vraie si toutes les places ontkjetonsdeadlockvraie si aucune transition franchissable
Exemples de propriétés
M(P1) + 3 × M(P2) >= 3
(M(P3) and M(P4)) or M(P2)
markingBounded(1)
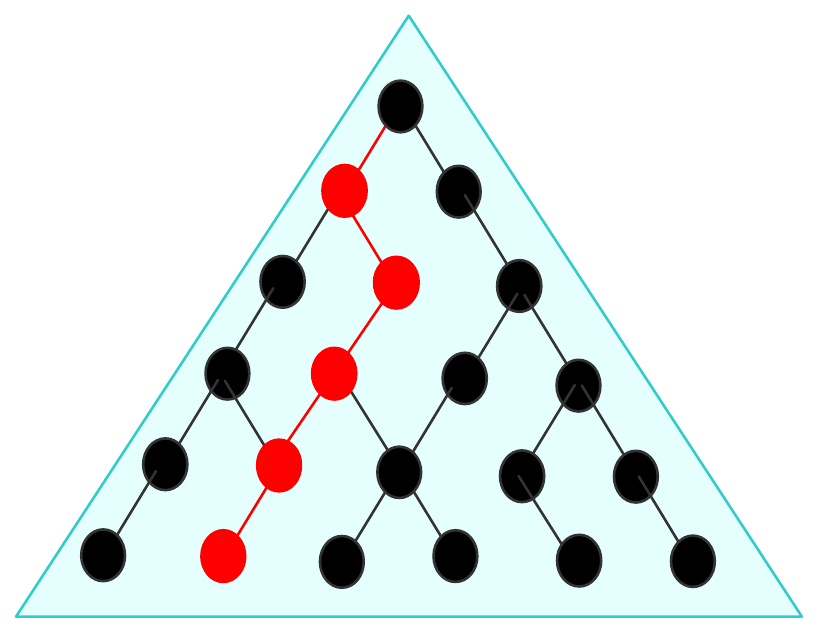
CTL
Représentation en arbre de
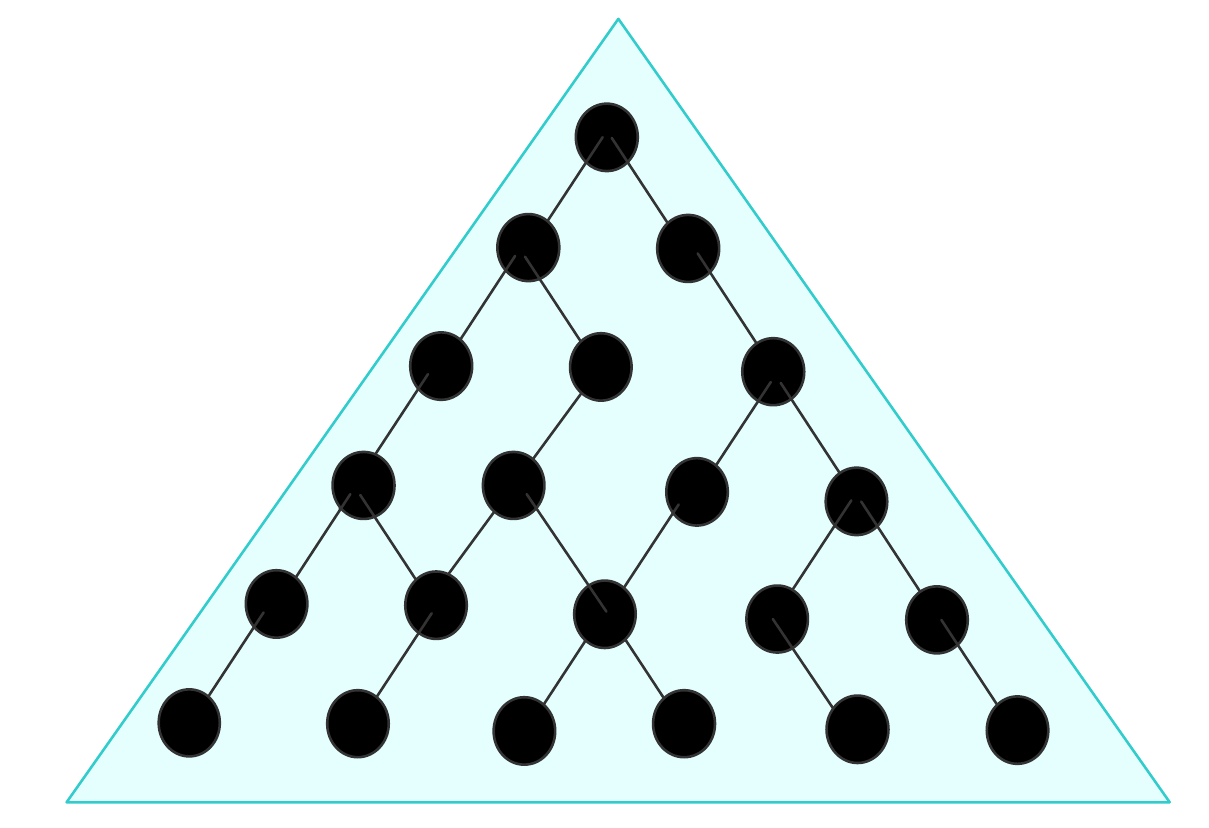
- l’état actuel du système (à la racine)
- et ses états futurs pour les noeuds enfants
Pour un réseau de Petri : arbre des marquages
Quantificateurs CTL 1/2
- A = along All paths
- toutes les branches doivent satisfaire la formule
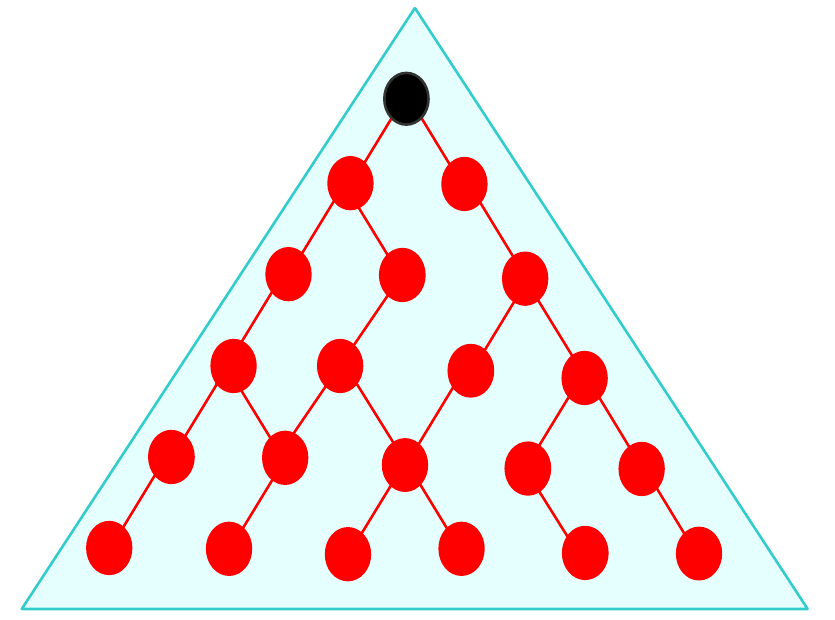
Quantificateurs CTL 2/2
- E = there Exists a path
- il doit exister une branche (au moins) qui satisfait la formule
Qualificateurs CTL
- F = Finally
- doit être satisfaite par au moins un état dans la branche
- G = Globally
- doit être satisfaite par tous les états de la branche
- X = neXt
- dans l’état suivant de la branche
- U = Until
- la première formule doit être satisfaite par tous les états de la branche jusqu’à ce que la deuxième formule devienne vraie à un moment
Visuel des combinaisons
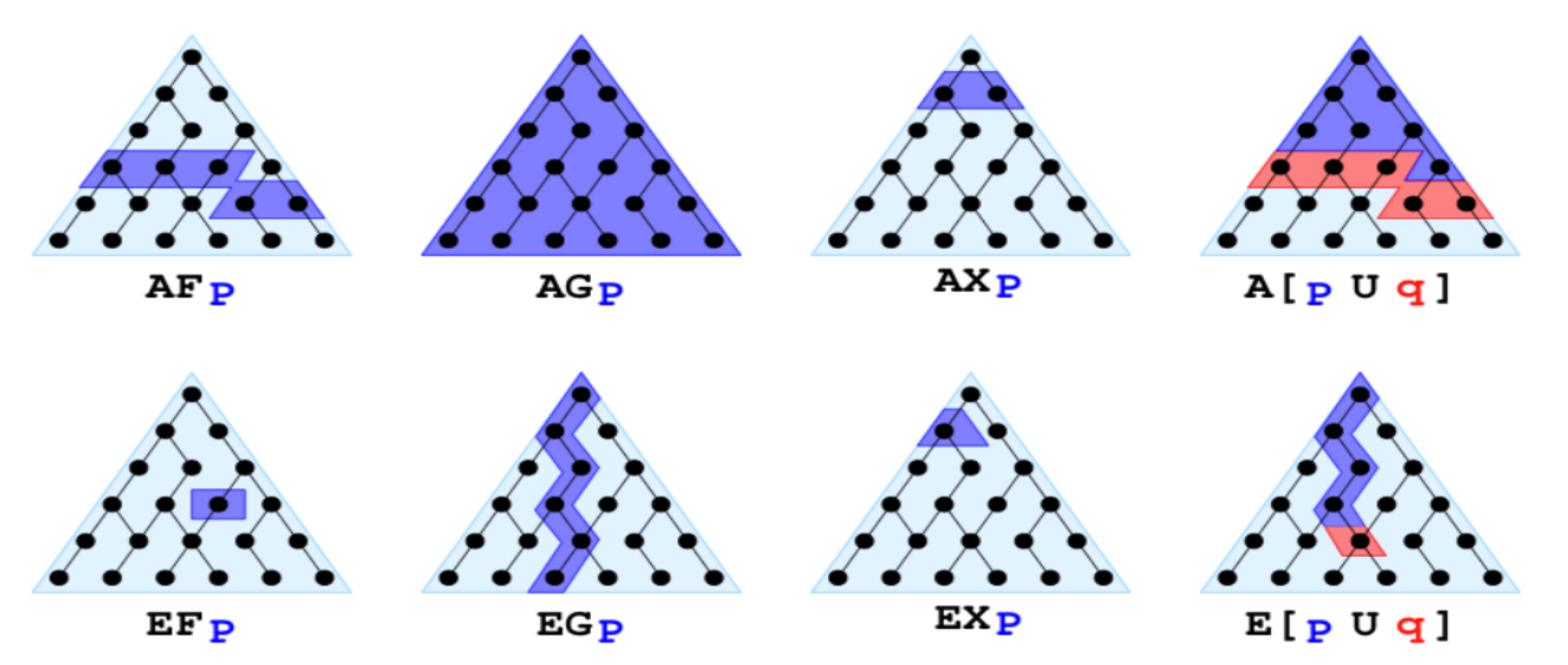
Liste propriétés temporelles 1/2
| Forumle | Quantificateur | Qualificateur |
|---|---|---|
| AFφ | dans toutes les branches | il y a un état qui satisfait φ |
| AGφ | tous les états satisfont φ | |
| AXφ | le deuxième état satisfait φ | |
| A[φ U ψ] | il y a un état qui satisfait ψ et tous les états avant satisfont φ |
Liste propriétés temporelles 2/2
| Forumle | Quantificateur | Qualificateur |
|---|---|---|
| EFφ | il existe une branche | il y a un état qui satisfait φ |
| EGφ | tous les états satisfont φ | |
| EXφ | le deuxième état satisfait φ | |
| E[φ U ψ] | il y a un état qui satisfait ψ et tous les états avant satisfont φ |
Exemples de propriétés complète
AF (M(P1) + 3 × M(P2) >= 3)
EF((M(P3) and M(P4)) or M(P2))
EX(markingBounded(1))
Exemple d’imbrication
EF(AG) (there Exists a path / Finally / along All paths / Globally)
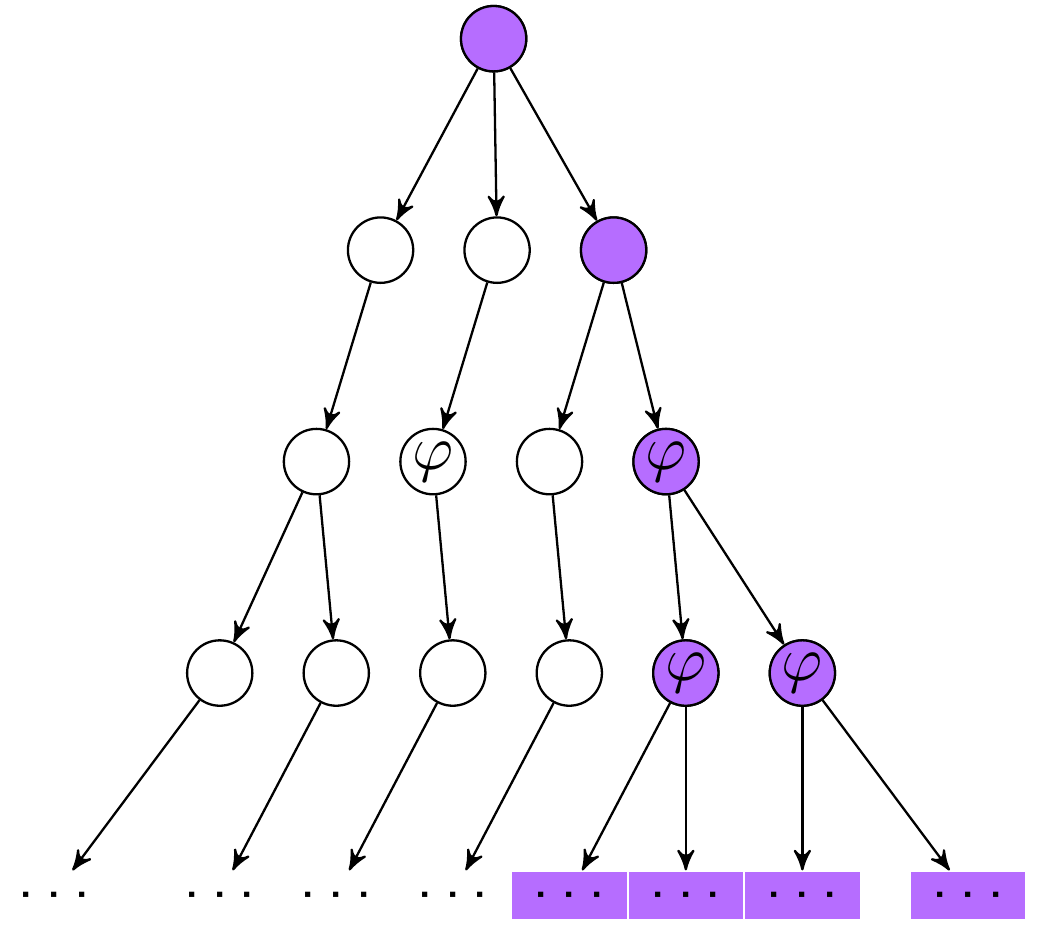
Exemple de tous les jours
Formule φ = “J’aime le chocolat”
- AGφ: “J’aime le chocolat maintenant et pour toujours, quelque soit mon futur”
- EFφ: “Il est possible que j’aime un jour le chocolat”
- AF(AGφ): “Je finirai par aimer soudainement le chocolat pour le reste de ma vie”
- AG(AFφ): “Je finirai toujours par aimer le chocolat même temporairement”
Roméo
Nous allons utiliser le model-checker Roméo
Roméo utilie un CTL allégé :
- pas de EX, AX
- pas de formules imbriquées
Tutoriel Roméo 1/2
Partie 2
Propriétés sur les transitions ?
Comment exprimer “la transition T n’est jamais franchissable” ?
La transition n'est pas franchissable si nous n'avons jamais ses places d'entrée qui contiennent en même temps un tokenAG(M(P1)==1 and M(P2)==1)
Propriétés sur les transitions ?
Comment exprimer “la transition T2 n’est jamais franchie avant T1” ?
Il faut créer un sous-réseau observateur pour vérifier que cela n’arrive jamais
Sous-réseau observateur
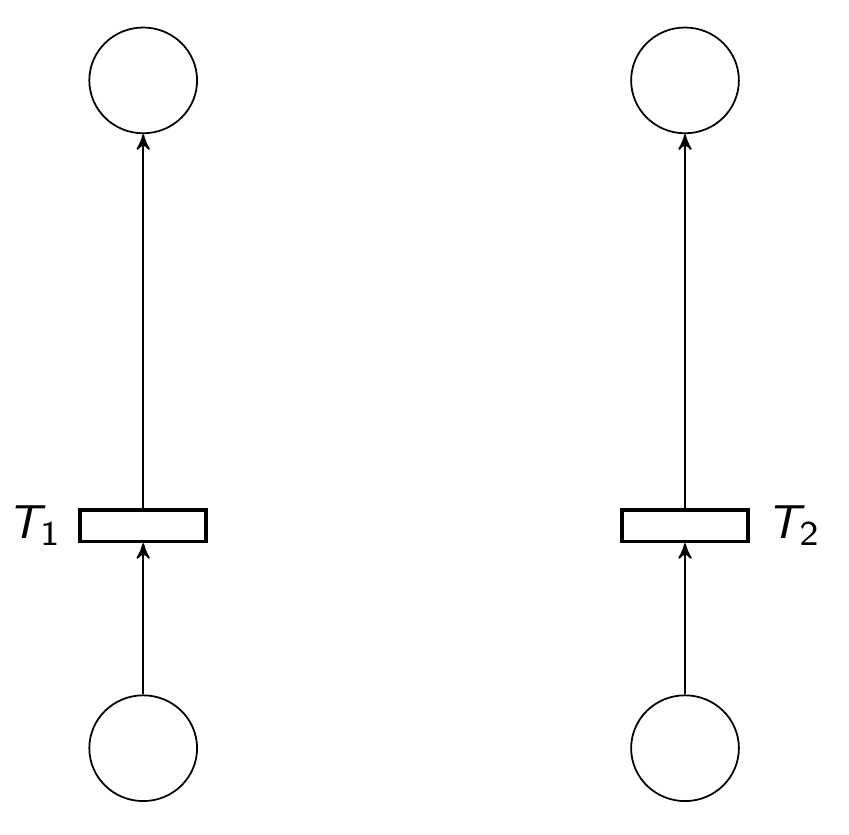
Sous-réseau observateur
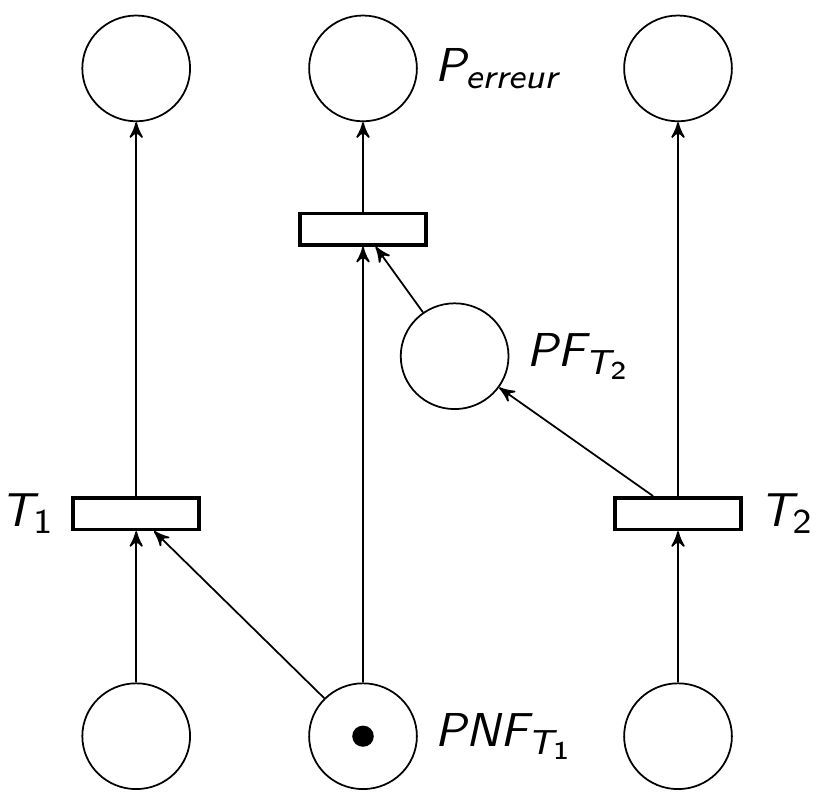
AG(M(Perreur ) == 0)
Attention on mélange système et vérification !
Arc lecteur
- arc entrant (entre place et transition)
- les jetons ne sont pas consommés lors du franchissement de la transition
Arc inhibiteur
- arc entrant (entre une place et transition)
- la transition n’est pas franchie si la place contient des jetons
Arc réinitialisateur
- arc sortant (entre une transition et une place)
- lorsque la transition est franchie le nombre de jetons dans la place sortante passe à 0
Priorités sur les tansitions
Il est possible de donner des priorités sur les transitions dans Roméo
La transition avec le plus grand chiffre sera franchie en premier
Réseaux de Petri temporisés
- extension qui ajoute du temps réel
- pour chaque transition un intervalle de temps est indiqué
- chaque transition est équipée d’une horloge
- la transition n’est franchissable que lorsque l’horloge est dans l’intervalle
Réseaux de Petri temporisés
- un RdP standard est équivalent à un RdP temporisé où tous les intervalles sont [0,∞[
- les conditions d’horloge empêchent certaines executions
- élagage de certaines branches des futurs possibles